
|
Tallinn University of Technology
Department of Cybernetics
Laboratory of Solid Mechanics
|
|
Title
|
Modeling a vibrating string terminated against a bridge with arbitrary geometry
|
|
Authors
|
Dmitri Kartofelev, Anatoli Stulov
Centre for Nonlinear Studies, Institute of Cybernetics at Tallinn University of Technology, Tallinn, Estonia
|
|
|
Heidi-Maria Lehtonen, Vesa Välimäki
Aalto University, School of Electrical Engineering, Department of Signal Processing and Acoustics, Espoo, Finland
|
|
Abstract
|
This paper considers dynamic string motion in which the displacement is unilaterally constrained by the termination condition with an arbitrarily chosen geometry. A digital waveguide model is proposed for simulating the nonlinearity inducing interactions between the vibrating string and the contact condition at the point of string termination. The current work analyzes the resulting string motion influenced by the contact conditions with mostly flat but slightly curved geometries. The effect of a minute imperfection of the termination condition on the string vibration is investigated. It was shown that the lossless string vibrates in two distinct vibration regimes. In the beginning the string starts to interact in a nonlinear fashion with the bridge, and the resulting string motion is nonperiodic. The duration of that vibration regime depends on the geometry of the bridge. After some time of nonperiodic vibration, the string vibration settles in a periodic regime. Presented results are applicable for example in the physics-based sound synthesis of stringed musical instruments, such as the shamisen, biwa, sitar, tambura, veena or even the bray harp and the grand piano.
|
|
Status
|
The manuscript was presented at the Stockholm Music Acoustics Conference 2013 (SMAC 2013)
|
|
Bridge geometry
|
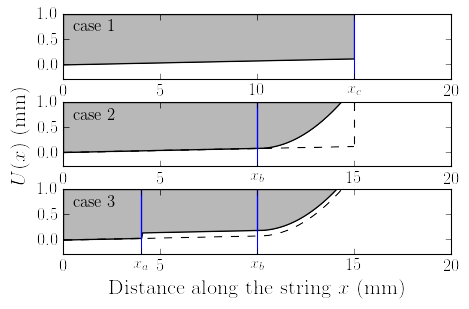
|
|
Fig. 1. Termination condition geometry for the cases under study. Solid vertical lines mark the positions of the characteristic values xa, xb and xc. Case 1: linear bridge with a sharp edge. Case 2: linear bridge with a curved edge, the dashed line shows the profile of the case 1 for comparison. Case 3: bridge with a small geometric imperfection, the dashed line shows the case 2 for comparison.
|
|
Slightly curved bridges of the lutes such as the shamisen, biwa, sitar, tambura and veena are usually located at the far end of the neck. Similarly the geometric contact condition (TC), in the presented model, is located at the termination point of the vibrating string x = 0.
|
|
Case 1: Linear bridge with a sharp edge
|
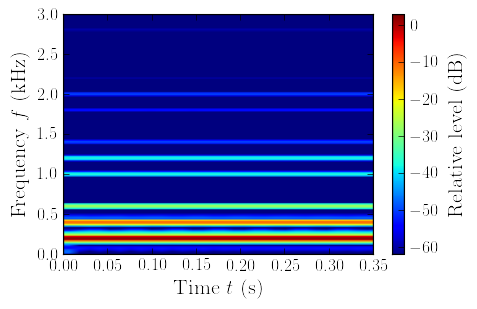 
|
|
Fig. 2. Left: Spectrogram of the signal u(l, t) for the linear case (no TC). Right: Spectrogram of the signal u(l, t) for the case 1. The transition between nonperiodic and periodic vibration regimes at t = tnp is shown using dashed line.
|
|
Animation of the dynamic motion of the string: Case 1
|
|
Case 2: Linear bridge with a curved edge
|
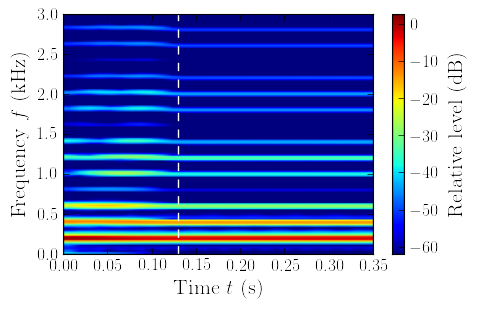
|
|
Fig. 3. Left: Spectrogram of the signal u(l, t) for the linear case (no TC). Right: Spectrogram of the signal u(l, t) for the case 2. The transition between nonperiodic and periodic vibration regimes at t = tnp is shown using dashed line.
|
|
Animation of the dynamic motion of the string: Case 2
|
|
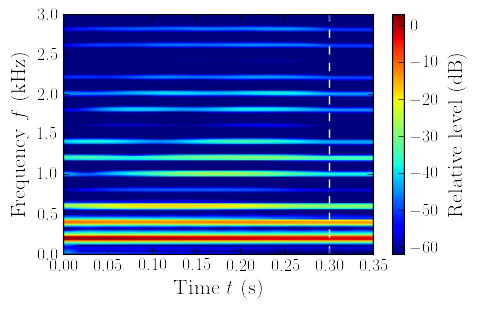
Case 3: Bridge with a small geometric imperfection
|
|
|
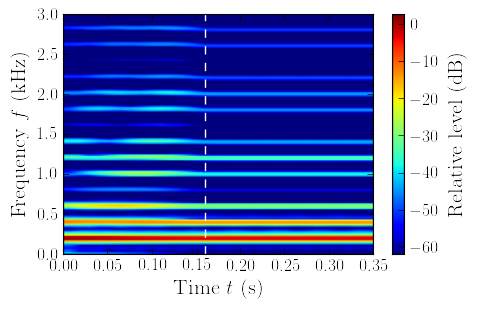
Fig. 4. Left: Spectrogram of the signal u(l, t) for the linear case (no TC). Right: Spectrogram of the signal u(l, t) for the case 3. The transition between nonperiodic and periodic vibration regimes at t = tnp is shown using dashed line.
|
|
Animation of the dynamic motion of the string: Case 3
|
|
Numerical implementation
|
|
Main iterative loop of the computer code that implements the bridge-string interaction model and the vibration of the ideal string. Code is written using Python programming language.
|
|
Code script: Code.pdf
|
|
Presentation slides used at SMAC 2013
|
|
Slides of the presentation given at the SMAC 2013 with embedded audio file and video animations.
|
|
Slides: Slides.pdf
|
|
Conclusions
|
This article introduced a model that simulates the vibration of an ideal string terminated against a bridge with an arbitrary geometry. Additionally, a method for modeling the effect of minute geometric imperfections of the bridge geometry on the string vibration was presented. It was shown that the lossless string vibrates in two distinct vibration regimes. In the beginning the string starts to interact in a nonlinear fashion with the bridge, and the resulting string motion is nonperiodic. After some time of nonperiodic vibration, the string vibration settles in a almost periodic regime, where the dynamic motion of the string is repetitious in time.
The duration of the nonperiodic vibration regime depends on the geometry of the termination. It was concluded that minor imperfection of the bridge profile geometry elongate the duration of the nonperiodic vibration regime and produce noticeable changes in the evolution of the timber in the nonperiodic regime of vibration. The resulting spectrum in the periodic regime is identical for all nonlinear cases studied. Comparison of the resulting spectra in the periodic vibration regime of the linear and nonlinear cases showed that the interaction of the string with the rigid bridge widens the spectrum by transferring energy from lower to higher vibration modes.
|
This work was conducted in February - April 2013, when Dmitri Kartofelev was visiting Aalto University. His visit was supported by the Kristjan Jaak Scholarship program from the Archimedes Foundation, Estonia.
This research was partly supported by the European Union through the European Regional Development Fund and by the Estonian Ministry of Education and Research (SF 0140077s08).
The work of Heidi-Maria Lehtonen was supported by the Finnish Cultural Foundation.
The authors are grateful for the useful comments and suggestions from Dr. Balázs Bank.
|




|
Modeling a vibrating string terminated against a bridge with arbitrary geometry
|







