
|
Tallinn University of Technology Department of Cybernetics Laboratory of Solid Mechanics |
| Title | Propagation of deformation waves in wool felt |
| Authors |
Dmitri Kartofelev, Anatoli Stulov Centre for Nonlinear Studies, Institute of Cybernetics at Tallinn University of Technology |
| Abstract | The natural wool felt is becoming increasingly popular and important as a resource material in various applications. In this study a constitutive equation that describes the deformation wave propagation in the felt material is derived using hysteretic piano hammer model. A nonlinear partial differential equation with third order terms that takes into account the elastic and hereditary properties of a microstructured felt is used to study a pulse propagation for the one-dimensional case. The boundary value problem is considered and the numerical solution describing the strain wave propagation is provided. It is shown that the speed of a deformation wave increases with the growth of its amplitude. Also the nonlinearity makes the front slope of a pulse steeper, which causes the eventual breaking of a pulse. The solution of the linear problem is analyzed, and the rate of the wave attenuation in the felt material is estimated. |
| Status | The manuscript is submitted for publishing to the journal Acta Mechanica |
| |
Animations of numerical solutions | |
|
Numerical solution of boundary value problem Linear case and amplitude decay |
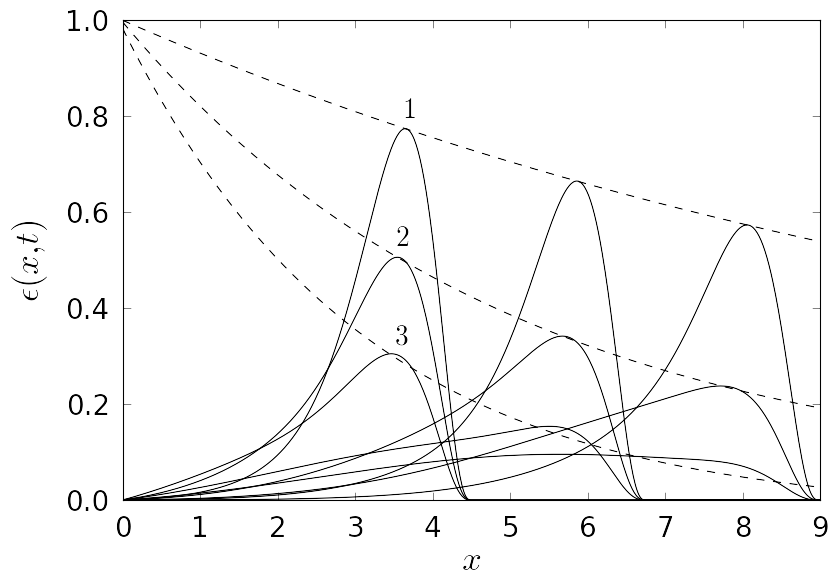
| The animation of the solution of the boundary value problem for the linear case (shown by solid line) and a corresponding pulse amplitude decay (shown by dashed line), where δ = 0.2 and boundary value parameter t0 = 1/2. The animation corresponds to a pulse 2 shown in Fig. 1. |
|
|
Figure 1. Snapshots of a pulse profiles shown for time moments t = 4.5, t = 6.75 and t = 9.0, varying the parameter δ. The boundary value parameter t0 = 1/2. The dashed lines show the amplitude decay. For a pulse 1 (δ = 0.8) the corresponding amplitude decay function is Exp(-0.08x); for a pulse 2 (δ = 0.5) the amplitude decay function is Exp(-0.20x); for a pulse 3 (δ = 0.2) the amplitude decay function is Exp(-0.32x). |
| Nonlinear case and variation of parameter p |
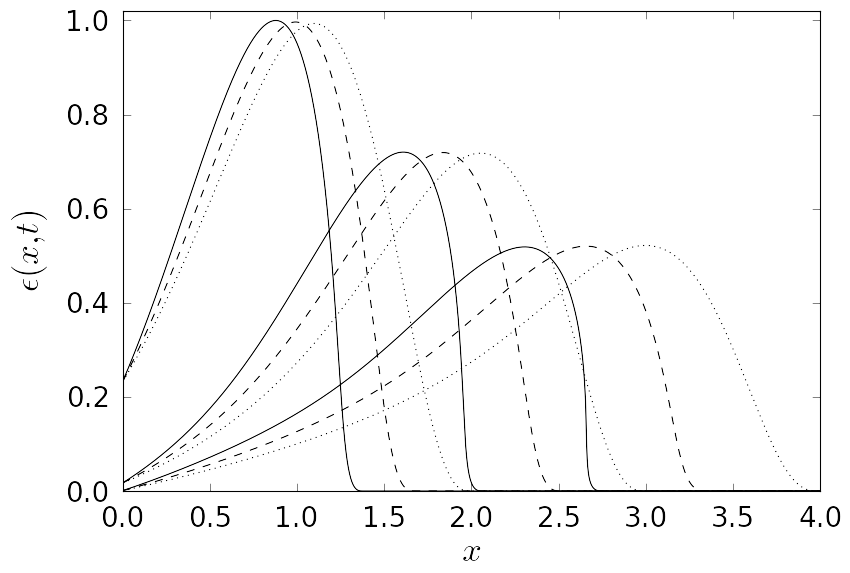
| The animation of the evolution of an initial boundary value pulse for the nonlinear case. The effect of varying the nonlinearity parameter p is shown. The animation corresponds to Fig. 2 presented below. |
|
|
Figure 2. Evolution of a nonlinear pulse (t0 = 1/2, A = 0.1) for three sequential time moments t = 2, t = 3 and t = 4. Material parameters selected δ = 0.2, p = 1.5 shown by solid line, p = 1.25 shown by dashed line, p = 1.0 (linear case) shown by dotted line. Results are normalized. |
| Nonlinear case and variation of amplitude A of initial disturbance |
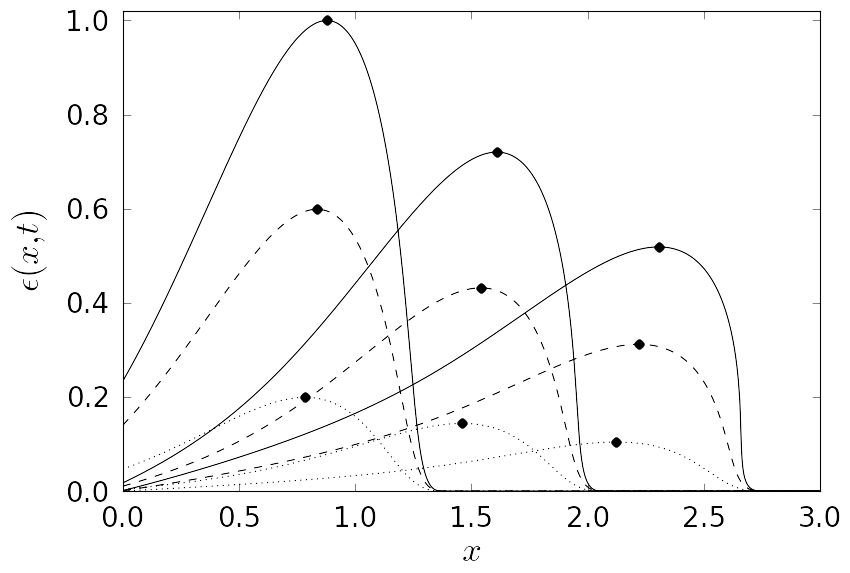
| The animation of the evolution of an initial boundary value pulse for the nonlinear case. The effect of varying the initial amplitude of the boundary value A is shown. The animation corresponds to Fig. 3 presented below. |
|
| Figure 3. Evolution of a nonlinear pulse (t0 = 1/2) for three sequential time moments t = 2, t = 3 and t = 4. Material parameters selected δ = 0.2, p = 1.5, initial amplitude A = 0.1 shown by solid line, A = 0.06 shown by dashed line, A = 0.02 shown by dotted line. Bullet show the position of the maximum. Results are normalized. |
| Conclusions |
|
We have derived a nonlinear constitutive equation of microstuctured wool felt based on the experimental results of piano hammers testing. Using this model, the boundary value problem that describes the propagation of deformation waves in the felt material is considered in current study. In case of the linear felt-type material, the dispersion analysis of the model is carried out, and the dependencies of the phase and group velocities on the felt parameters are obtained. It is shown that the group velocity is always greater than the phase velocity, and therefore the wool felt is a medium with anomalous dispersion.
The numerical solution of the linear boundary value problem is used to estimate a strain pulse amplitude decay during its propagation through the felt. It is shown that in the linear case the decay constants may be obtained rather accurately by using dispersion analysis. A strain pulse propagation in nonlinear felt is also considered. The general influence of the nonlinear parameter p on a pulse evolution is investigated. It is concluded that the front of a pulse becomes steeper as it propagates through the felt material, and that this pulse steepening increases with growth of the value of the parameter p. The effect of an initial pulse amplitude A on the nonlinear wave propagation is simulated. It is shown that for greater amplitudes the maximum point or the crest of a pulse propagates faster than the front of a pulse. This is related to the fact that the group velocity is greater than the phase velocity, and confirms our assumptions about the felt as a medium with anomalous dispersion. It is revealed that the front slope of a pulse is strongly determined by a pulse amplitude A. Such a process results in the formation of the shock wave, which is directly caused by the nonlinear features of the microstuctured felt material. The originality of presented model is expressed in the fact that the parameter p that describes the felt nonlinearity may be any real number greater than 1, including the non-integer values. The solution of the novel wave equations (18), (19) reflects many physical effect as demonstrated in this paper. In conclusion, we may state that the wool felt is a strongly dissipative and dispersive nonlinear medium, with a strong damping effect. |
| |
Acknowledgments | |
|
This research was supported by the EU through the European Regional Development Fund, and by the Estonian Ministry of Education and Research (SF 0140077s08). The authors would like to thank Prof. Aleksander Klauson from Tallinn University of Technology for his assistance in the stress-strain testing of the felt pads. |
|
Propagation of deformation waves in wool felt