
|
Tallinn University of Technology Department of Cybernetics Laboratory of Solid Mechanics |
| Title | Wave propagation and dispersion in microstructured wool felt |
| Authors |
Dmitri Kartofelev, Anatoli Stulov Centre for Nonlinear Studies, Institute of Cybernetics at Tallinn University of Technology |
| Abstract | On the basis of the experimental data of the piano hammers study the one-dimensional constitutive equation of the wool felt material is proposed. This relation enables deriving a nonlinear partial differential equation with third order terms, which that takes into account the elastic and hereditary properties of a microstructured felt. This equation of motion is used to study pulse evolution and propagation in the one-dimensional case. The thorough analysis both of the linear and nonlinear problems is presented. The physical dimensionless parameters are established and their importance in describing the dispersion effects is discussed. It is shown that both normal and anomalous dispersion types exist in the wool felt material. The dispersion analysis shows also that for the certain ranges of physical parameters negative group velocity will appear. The initial value problem is considered and the analysis of the numerical solution describing the strain wave evolution is provided. The influence of the material parameters on the form of a propagating pulse is demonstrated and explained. |
| Status | The manuscript is submitted for publishing to the journal Wave Motion |
| |
Animations of numerical solutions | |
|
Numerical solution of initial value problem Linear case, a symmetrical pulse evolution |
| The animation of the solution of initial value problem for the linear case. The effect of varying the parameter δ is demonstrated. The animation correspond to Fig. 1. presented below. |
|
|
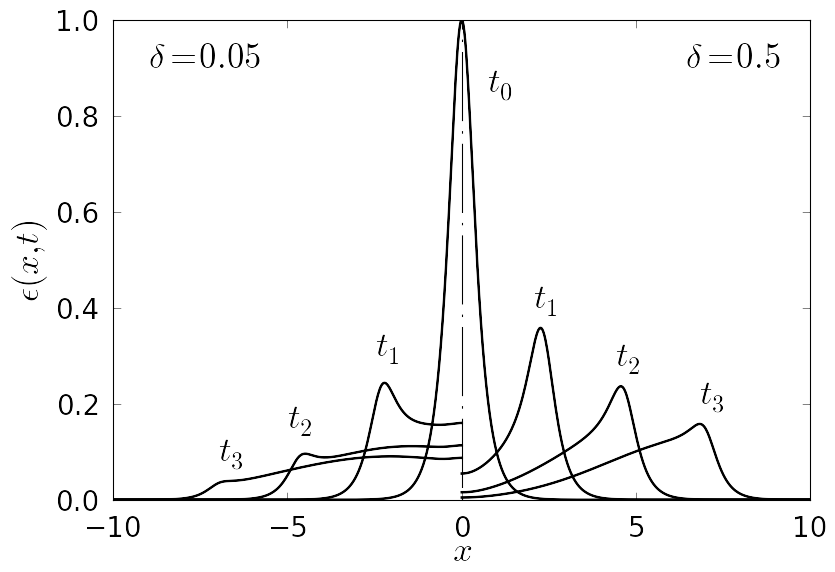
Figure 1. Snapshot of a pulse profile, where A = 1 and α = 3, shown for time moments t0 = 0, t1 = 7/3, t2 = 14/3, and t3 = 21/3 calculated for two different values of the parameter δ. |
| Linear case, an asymmetrical pulse evolution |
| The animation of the evolution of an initial value pulse with two characteristic dominant fundamental frequencies. The animation corresponds to Fig. 2 presented below. |
|
|
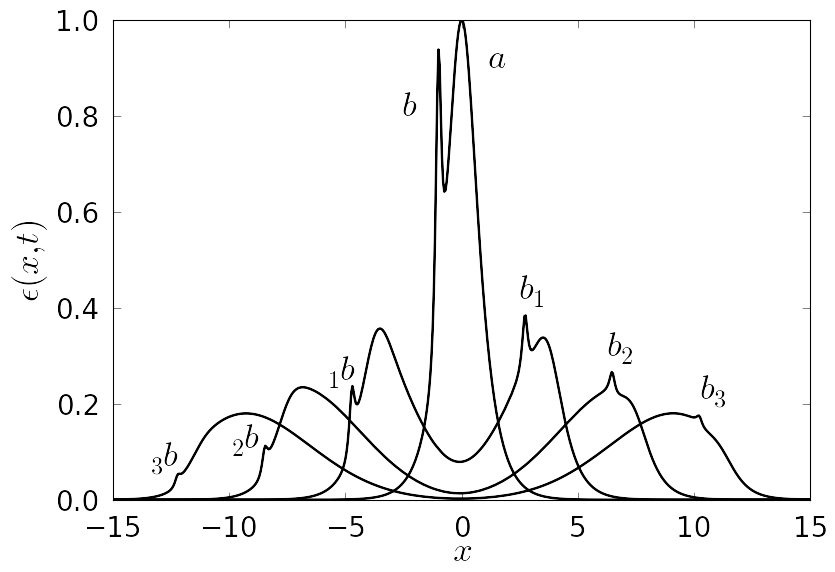
Figure 2. Snapshot of a pulse profile, where δ = 0.5, α = 1.6, β = 10, A = 1 and B = 0.55, shown for time moments t0 = 0, t1 = 15/4, t2 = 30/4, t3 = 45/4. Marks bi indicate the position of peak b moving to the right, and marks ib indicate the position of peak b moving to the left. |
| Nonlinear case, influence of parameter p |
| The animation of the evolution of an initial value pulse for the nonlinear case. The effect of varying the parameter p value is shown. The animation corresponds to Fig. 3 presented below. |
|
|
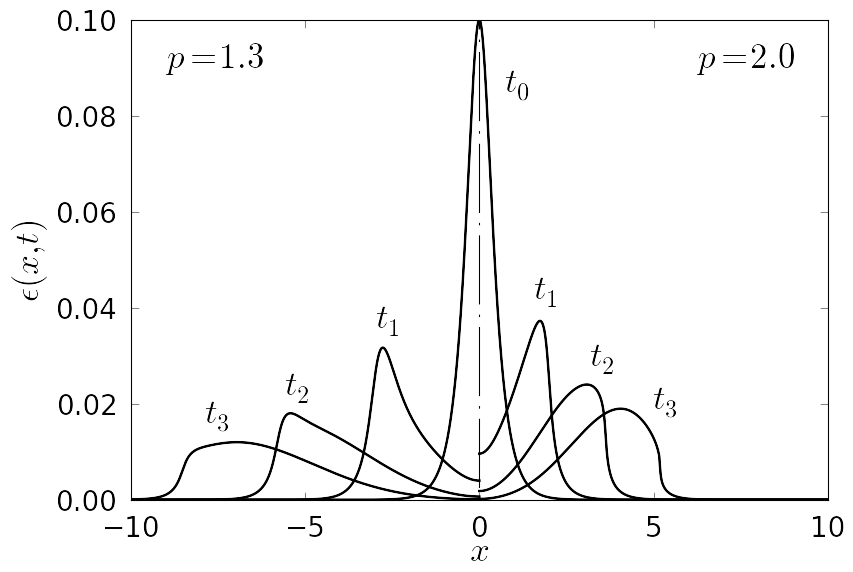
Figure 3. Snapshot of a pulse profile, where δ = 0.5, α = 3 and A = 0.1, shown for time moments t0 = 0, t1 = 10/3, t2 = 20/3, t3 = 30/3, calculated for two different values of the parameter p. |
| Nonlinear case, influence of amplitude A |
| The animation of the evolution of an initial value pulse for the nonlinear case. The effect of varying the initial amplitude of the initial value A is shown. The animation corresponds to Fig. 4 presented below. |
|
|
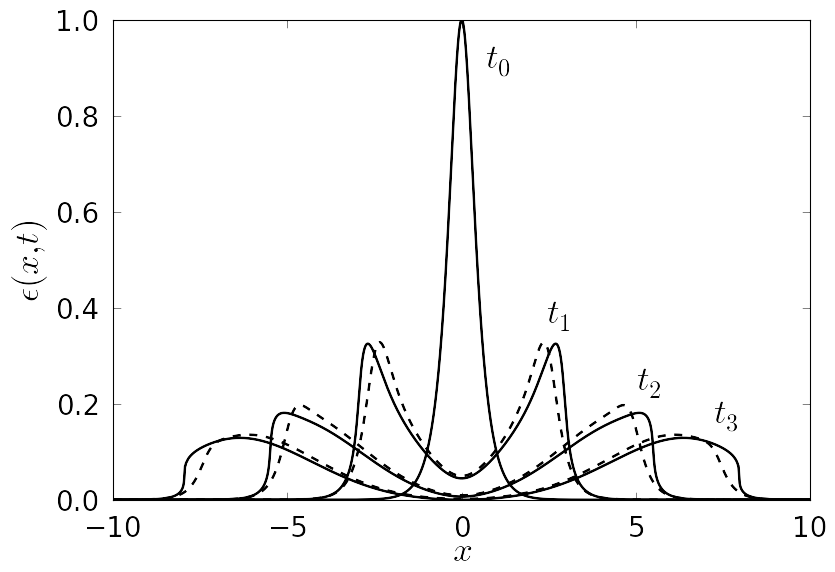
Figure 4. Normalized snapshots of a pulses' profiles, where α = 3, δ = 0.5 and p = 1.45, shown for time moments t0 = 0, t1 = 10/3, t2 = 20/3, t3 = 30/3. The profiles with initial amplitude A = 0.2 are shown by solid line. The profiles with initial amplitude A = 0.02 are shown by dashed line. |
| Conclusions |
|
The nonlinear felt model, which takes into account the elastic and hereditary properties of the microstructured felt was used to study the strain pulse evolution in the one-dimensional case. The linear and nonlinear analysis of the model was presented.
The dispersion analysis of the linear problem showed that normal and anomalous dispersion types can exist in the wool felt material. The analysis of the influence of material parameters on the dispersion behaviour was presented. It was shown that for some values of the parameters the restrictive band-gap or the negative group velocity region or both appeared. The negative group velocity emerged always in connection with the region of normal dispersion. With the aid of the numerical solution of the initial value problem these dispersion phenomena were demonstrated. The nonlinear effects of the general influence of the nonlinearity parameter p and the amplitude of the initial disturbance were demonstrated. It was shown that for the higher value of the parameter p the front of an evolving pulse become steeper, and this phenomenon was intensified with the growth of the value of the parameter p. Also, it was shown that the front slope of the evolving pulse was strongly determined by the pulse amplitude. A greater initial amplitude forced the maximum point of the peak to propagated faster than the front of the pulse. Therefore, these nonlinear effects were eventually responsible for formation of the discontinuity at the pulse front and appearance of the shock wave. In conclusion, this paper presented the solution of a novel wave equation, which reflected many physical effects of the microstructured wool felt. The most dominating feature of the felt was shown to be the strong damping effect on any wave evolving and propagating through it. |
| |
Acknowledgments | |
| This research was supported by the EU through the European Regional Development Fund, and by the Estonian Ministry of Education and Research (SF 0140077s08). The authors would like to thank Prof. Aleksander Klauson from Tallinn University of Technology for his assistance in the stress–strain testing of the felt pads. The authors gratefully acknowledge the valuable comments provided by Dr. Mihhail Klopov from Tallinn University of Technology on the topic of solving nonlinear problems using the FDM. |
|
Wave propagation and dispersion in microstructured wool felt